Encryption as Obfuscation

Some time ago, we analyzed a sample with an encrypted payload using an interesting technique. Unfortunately we can’t share the sample, and it isn’t available on Virustotal neither. In order to show this technique - and its weakness - we decided to write a simple program ourselves implementing something similar, though not identical. This test sample is available here - and we promise it does not contain any malicious code. If you run it, you’ll notice it doesn’t do anything. Under the right circumstances, it should decrypt an embedded payload and write it to a file output.dat. And of course, we’d like to find this decrypted data.

Let’s check the main() code at VA 0x140002410:

void FUN_140002410(void)
{
  ...
  nsize[0] = 100;
  GetComputerNameA((LPSTR)compName,nsize);
  FUN_140001e60(compName);
  noMatch = memcmp(compName,&compName_Hash,0x10);
  if (noMatch == 0) {
      ...
  }
  ...
}

Note we’re using Ghidra in this report, so it is easy to reproduce for everyone, but of course this also works perfectly in IDA Pro. Our sample seems to verify the computer name (GetComputerNameA()) by comparing it to a hardcoded 16 byte value. The function FUN_140001e60 probably implements some kind of hash function. Indeed, looking at it reveals an in-place MD5 hasher, which always uses 16 bytes of data to hash - this is also the reason the function has no size argument:

void FUN_140001e60(BYTE *param_1)
{
  ...
  // Data is assumed to be 16 bytes long, and output (MD5) is also 16 bytes
  hash_len[0] = 0x10;
  data_len = 0x10;
  if (hCryptProv == 0) { // hCryptProv is a global variable initialized to 0
    CryptAcquireContextW(&hCryptProv,(LPCWSTR)0x0,(LPCWSTR)0x0,PROV_RSA_FULL,CRYPT_VERIFYCONTEXT);
  }
  if (data_to_hash == (BYTE *)0x0) { // obviously called as destructor
    if (hCryptProv != 0) {
      CryptReleaseContext(hCryptProv,0);
    }
    hCryptProv = 0;
  }
  else { // actual data to hash
    CryptCreateHash(hCryptProv,CALG_MD5,0,0,&phHash);
    CryptHashData(phHash,data_to_hash,data_len,0);
    CryptGetHashParam(phHash,HP_HASHVAL,hash_data,hash_len,0);
    // copy hash over input data, both are 16 bytes in size
    for (idx = 0; idx < 0x10; idx = idx + 1) {
      data_to_hash[idx] = hash_data[idx];
    }
    CryptDestroyHash(phHash);
    phHash = 0;
  }
  ...
}

so we can rename it to e.g. MD5_16bytes(). As the code uses a simple compare to verify the identity of the system, we could try to patch the sample, e.g. by changing the == into a !=, i.e. by changing the JNZ instruction at VA 0x140002499to a JZ instruction. Feel free to try this out - you’ll notice that the sample still does not do anything useful, it simply crashes.

Examining the full address space of the binary (IDA’s navigation bar is very useful here) reveals the encrypted payload to be located at file offset 0xce70 or VA 0x14000F070. It is 323955 bytes long:

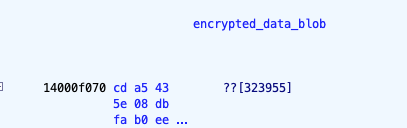
The most obvious thing to do at this point is to check code references to the encrypted payload. We find four references (some refactoring was already done by us):

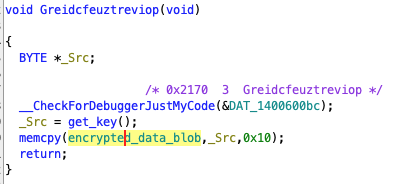
This code just seems to overwrite the first 16 bytes of our blob, so obviously not related to decryption. the code itself does not seem to make much sense though. Interestingly, a cryptic function name appears at the top - the function is actually exported under this name, which is unusual for an executable, but not impossible. If we check code references to the function itself, we don’t find any - is it called at all?

The second occurrence looks very similar and does not make much sense either, and also appears in another exported function without code reference.

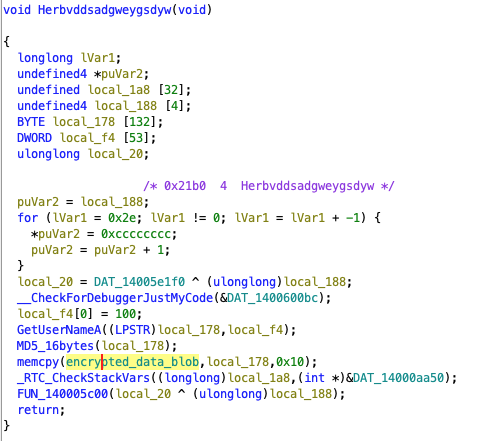
Same for the third one…

Finally, this fourth one - also in an exported function without code reference to it - looks more interesting. We see a function taking encrypted_data_blob() as first parameter, and its size as second parameter. The returned data is then written to a file (note that filename is set to a string output.dat somewhere else), so this function must be used for decryption. Let’s look into it:

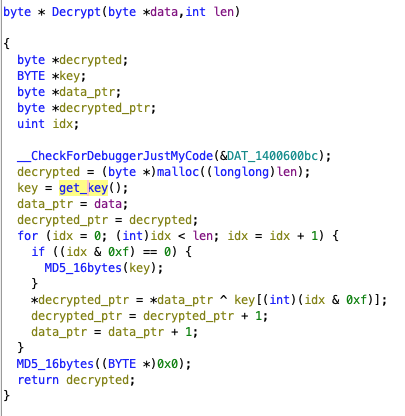
This is a cyclic XOR with a obviously 16 byte long key (returned by FUN_140001860(), renamed get_key() above). The key is changed after every round of 16 bytes using the MD5_16bytes() hasher we already analyzed. This key reset also happens at the very start (idx == 0).

The content of get_key() is a bit more complex:

It is not required to fully understand the code, but from the string SELECT * FROM Win32_ComputerSystemProduct and UUID further down, it becomes clear that the system UUID of the machine is extracted. So the binary is obviously tailored for one very specific system with one UUID, which in turn is used as an encryption key.

Our problem with this binary now is that we don’t know the UUID of the victim machine. On one hand, the encryption is very simple - if we could guess the first 16 bytes of the encrypted payload, we could calculate the key; but we have no idea about the actual content, it could be compressed without a standard header. Even knowing some plain text later in the payload - e.g. we could hope for a sequence of 0 bytes for instance - would not help neither, as the algorithm applies MD5_16bytes() to the key after each chunk of 16 bytes, which we can’t revert. And the key space, 128 bits, is too large for brute forcing. So, how can we decrypt the data blob?

We can hope that the Decrypt() might be called from another place as well, which might give us additional leverage. Unfortunately this is the only code reference to it. However, if we check the code references to get_key(), we’re more lucky. Besides the two hits we already know (get_key() also appeared in the Greidcfeuztreviop()export above), we see an exact copy of Decrypt() at address 0x140001770, which we’ll call decrypt() below; this function indeed has several code references of the same form:

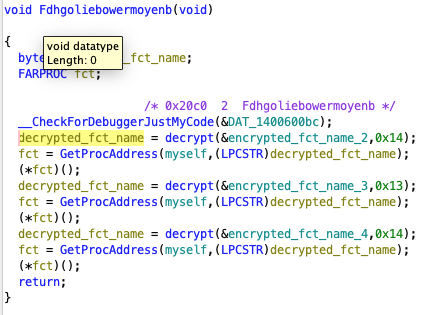
and

which is the mainfunction we already looked at before. These calls are interesting, as they all refer to the sample itself - GetModuleHandleW((LPCWSTR)0x0) returns a handle to it - and then use GetProcAddress() to find an exported function, which in turn is just called. The name is the result of the decryption using the very same key as used for the large encrypted payload. This also explains why the sample crashed after patching: with a wrong decryption key, GetProcAddress() returns a NULL pointer, and trying to call this will trigger an exception. This also explains why the sample exports some functions - it uses those to call these functions indirectly, and it will also hide code references to these functions. In return, these functions won’t expose any code reference. Usually, such a dynamic linking - which can also be done in more obscure ways - is a good and often used obfuscation technique. In this case, however, it is rather a weakness that opens the door to decrypt the payload, as we now have several good plain text and cipher text samples that we can use for a known plain text attack. The plain text candidates are simply all exported function names, which appear in the sample:

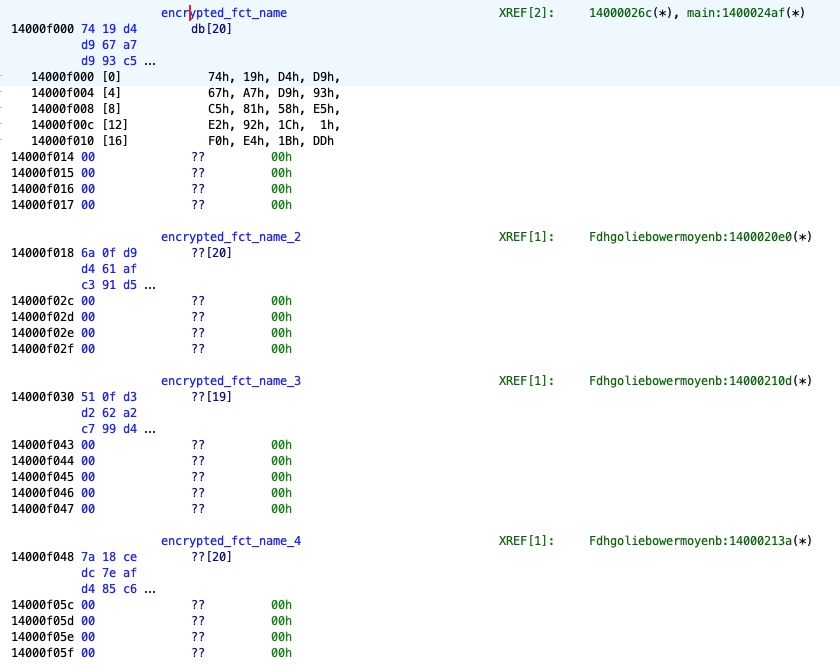
The cipher text candidates also appear in the sample:

For the actual cracker, we first implement the MD5_16bytes() and decrypt() functions in Python. Note that we do not apply MD5_16bytes() at loop entrance (since we can’t crack the actual key, but just the result after this initial MD5_16bytes() call), hence the “and idx>0”:

import hashlib  
  
  
def MD5_16bytes(key: bytes) -> bytes:  
    return hashlib.md5(key).digest()  
  
  
def decrypt(data: bytes, key: bytes) -> bytes:  
    res = bytearray()  
    for idx, c in enumerate(data):  
        if idx % 16 == 0 and idx > 0:  
            key = MD5_16bytes(key)  
        res.append(c ^ key[idx % 16])  
    return res

It is trivial to calculate (“crack”) the key given a known plain text and a cipher text of 16 bytes using a simple XOR:

def calc_key(data: bytes, clear: bytes) -> bytes:  
    keyBytes = bytearray()  
    for idx in range(16):  
        keyBytes.append(data[idx] ^ clear[idx])  
    return bytes(keyBytes)

For the cracking process, we just add all exported function names and encrypted blobs from the binary; we could use more advanced code to gain the data from the sample directly, but the manual process suffices as POC:

# Cleartext candidates are all exported function names  
candidates: list[bytes] = [b"Fdhgoliebowermoyenb\x00",  
                           b"Herbvddsadgweygsdyw\x00",  
                           b"Greidcfeuztreviop\x00",  
                           b"Xrejidsgreqweowustr\x00",  
                           b"Dsowieperdferutotyx\x00",  
                           b"croljiwosswoxwloxd\x00",  
                           ]  
# Ciphertexts are extracted from decryption function  
encrypted: list[bytes] = [  
    bytes((0x74, 0x19, 0xd4, 0xd9, 0x67, 0xa7, 0xd9, 0x93, 0xc5, 0x81,  
           0x58, 0xe5, 0xe2, 0x92, 0x1c, 0x01, 0xf0, 0xe4, 0x1b, 0xdd)),  
    bytes((0x6a, 0x0f, 0xd9, 0xd4, 0x61, 0xaf, 0xc3, 0x91, 0xd5, 0x8b,  
           0x5e, 0xf7, 0xf5, 0x90, 0x04, 0x0d, 0xe6, 0xfe, 0x0b, 0xdd)),  
    bytes((0x51, 0x0f, 0xd3, 0xd2, 0x62, 0xa2, 0xc7, 0x99, 0xd4, 0x9d,  
           0x58, 0xef, 0xe8, 0x88, 0x1f, 0x17, 0xed, 0xee, 0x79)),  
    bytes((0x7a, 0x18, 0xce, 0xdc, 0x7e, 0xaf, 0xd4, 0x85, 0xc6, 0x8a,  
           0x48, 0xf7, 0xf5, 0x86, 0x14, 0x0b, 0xf1, 0xf3, 0x0e, 0xdd)),  
]

We do not know which encrypted element belongs to which clear text candidate, and which clear text candidates are used at all,. The lengths could give us some hints, but is it easiest to try all combinations, then calculate the key in case the matching is right, and count all keys in a dictionary. This is possible because all clear and encrypted candidates are at least 16 bytes long:

# We count all key candidates (keys that can decrypt a cipher to a cleartext candidate)  
keys: dict[bytes, int] = {}  
  
# To populate, try all clear/cipher pairs (we do not know which fits which)  
for clear in candidates:  
    for cipher in encrypted:  
        key = calc_key(cipher, clear)  # This key could encrypt the first 16 bytes
        # Try full encryption:
        cipher2 = bytes(decrypt(clear, key))  
        if cipher2 != cipher:  
            continue  
        # we got a hit  
        if key not in keys:  
            keys[key] = 0  
        keys[key] += 1

Finally, we extract the most often used key and apply it to the large encrypted payload:

# choose the key with most hits  
chosen_key: bytes = sorted(keys.items(), key=lambda item: -item[1])[0][0]  
  
# And apply to data stored in a file 'xorIn.dat'  
with open('sample.exe', 'rb') as fh1:  
    data = fh1.read()[0xce70:][:0x4f173]  
  
data = decrypt(data, chosen_key)  
  
with open('output.dat', 'wb') as fh2:  
    fh2.write(data)

Inspection of the resulting data in output.dat will show the decryption succeeded.